Chord Construction Part 3 7th Chords And Beyond
![]()
Welcome back! If you have been following along in this mini series of chord construction lessons then you will remember in Part 1 how we stacked intervals of 3rds to build basic three note chords called triads and in Part 2 we learned about triad inversions. In this lesson we will continue stacking intervals to build even more chords! We will build chords like 7ths, 9ths and 11ths all of which are the basic chord types that are used to build chords found in Jazz, Rock as well as Classical music. These chords can be used on other instruments too, not just in guitar. So put your music theory swim suit on and let's dive in!
6th chords
To build a 6th chord you take either a Major or minor triad and add an interval of Major 6th above the root to it (a whole step above the 5th).
EX. Key of C Major(6th in orange)
Example: C6 chord - CEGA (a.k.a Am7 chord inversion see below)
Example: Dm6 chord - DFAB Bm7b5 (a.k.a Bm7b5 chord inversion see below)
If the third is a minor 3rd above the root the chord is a minor 6th chord.
If the 3rd is a Major 3rd above the root the chord is A Major 6th chord or just 6.
What happens if the 6th above root is minor? The chord is some form of 7th chord inversion (see below).
7th chords
A 7th chord is built by adding another interval of a 3rd on top of the basic triad. 7th chords are highly used for Blues and Jazz guitar chords.
All seventh chords in the key of C Major with color coded intervals

* The Delta symbol  is sometimes used for Major 7 chords to help distinguish it from Dominant 7 chords (the chord at the 5th scale degree).
is sometimes used for Major 7 chords to help distinguish it from Dominant 7 chords (the chord at the 5th scale degree).
* The chord that occurs on the 7th degree is called a Half diminished because the 7th is not a diminished 7th interval.
* Notice how Am7 and Bm7b5 chords have the same notes as C6 and Dm6? This shows that all 6th chords can be thought of as inverted 7th chords!
7th chord examples
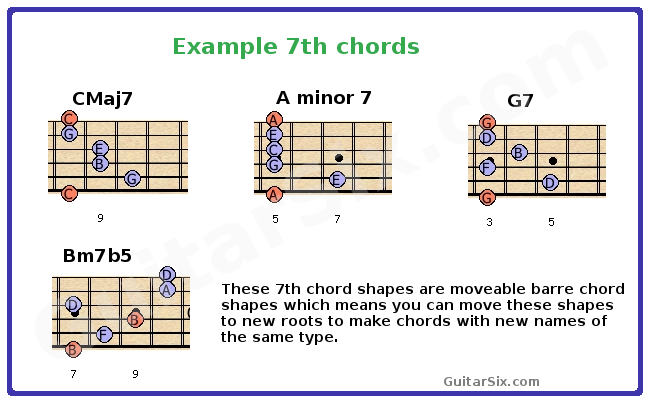
In the 7th chord examples above I only list the barre chords shapes for each type (in the C major scale) to save page space.
Extended chords
Extended chords are the chords you get when stacking intervals of a 3rd above the octave.
9th chords
Once you pass the root note octave and continue stacking in 3rds, The first note you hit is the 9th (which is the same as the second just an octave higher). A true 9th chord has an interval of a Major 9th on top of a Major or minor 7th chord.
Some notes of the 9th chord frequently get left out during play time in order to make them easier/possible to play on the guitar. The notes left out usually get played by other instruments or not at all.

* I have never read a music theory or chord dictionary book that listed the 9th chords that occur on the iii and Vii chord. They are interesting beasts consisting of a minor 9th interval stacked on top of minor 7th intervals. What I am calling them here is Em7b9 (notes EGBDF) and Bmin7(b5,b9) (notes BDFAC). They exist but are not commonly used.
9th chord examples
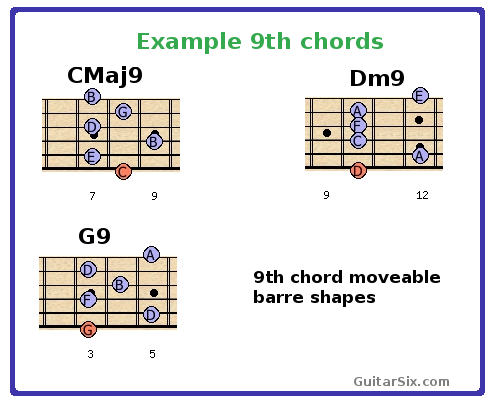
There is no such thing as 10th or 12th chords because the 3rd is still the 3rd and the 5th is still the 5th.
11th chords
11th chords formed by adding an interval of an 11th (the 4th an octave higher than the root) to a 9th chord. Just like the with 9th chord, some tones are usually omitted in order to be able to play them on the guitar. The tones usually omitted are 3rd or 5th or 9th.
13th chords13th chords add the 6th an octave higher than the root to the 11th chord. Again chord tones like the 3rd or 5th or 9th can be left out.
* I'm not giving 11th and 13th chord examples here because frankly if you find yourself in need of using them (like in Jazz) then you are probably to the point in your playing where you are making up your own shapes!
Suspended chords
Suspended chords are chords where the third is replaced by either the 2nd or the 4th. Suspended chords are neither Major or minor because they have no 3rd.
Examples:
Csus2 chord = CDG.
Csus4 chord = CFG

Summary
Whew....that was a lot of information to soak in! By now you should have some good chord building skills under your belt. I have to remind you that for this lesson we have only been building chords using the intervals of the Major/minor scales. There are many more types of chords you can build using the rules learned here and altering them.
At some point in the future I will do a lesson that talks about those chords. But for now you should be well equipped to build your own common chord types. I encourage you to look through a chord dictionary and figure out the construction of the chords that you have never seen before. I hope this lesson has inspired you to learn even more. Until the next lesson....
Posted August 27, 2015, 5:08 pm in: Guitar lessons
Share a link to this guitar lesson with your friends (right click Permalink > copy or mobile long press > copy)



